“A common practice among engineers is to put together a prototype of an assembly with every part very close to the nominal or intended measured characteristic. The test may go off well. The problem is that when the assembly goes into production, all characteristics will vary.” W.E. Deming, American engineer and statistician who championed statistical process control.
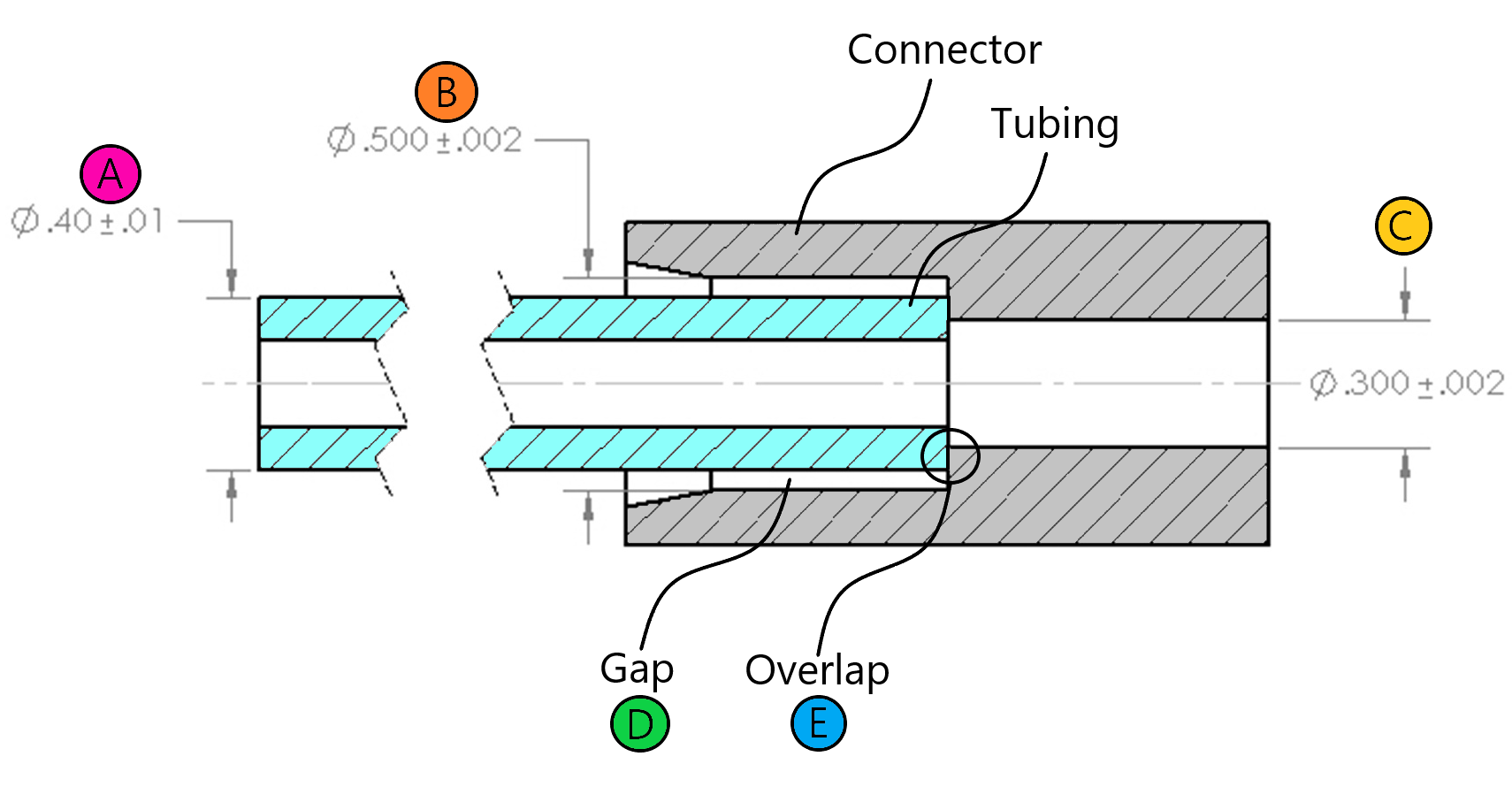
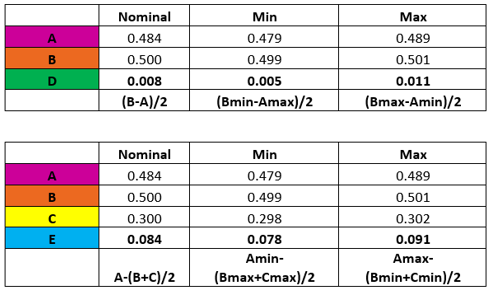
In medical device design a common scenario to assess is the fit between tubing and some kind of connector. In the example shown here, there is an extruded PVC tubing that is inserted into an injection molded polycarbonate connector. It is required that there be a gap present between the OD of the tubing and the ID of the connector to make room for adhesive: too small of a gap and there won’t be enough adhesive for a sufficiently strong bond, too large of a gap and the adhesive may not cure properly. A typical range for UV adhesive, for example, is .007”-.010”/side. In addition, it is required that there be an overlap between the OD of the tubing and the shelf at the transition from the large ID of the connector to the small ID of the connector. For this example, we will set this overlap requirement to be a minimum of .010”.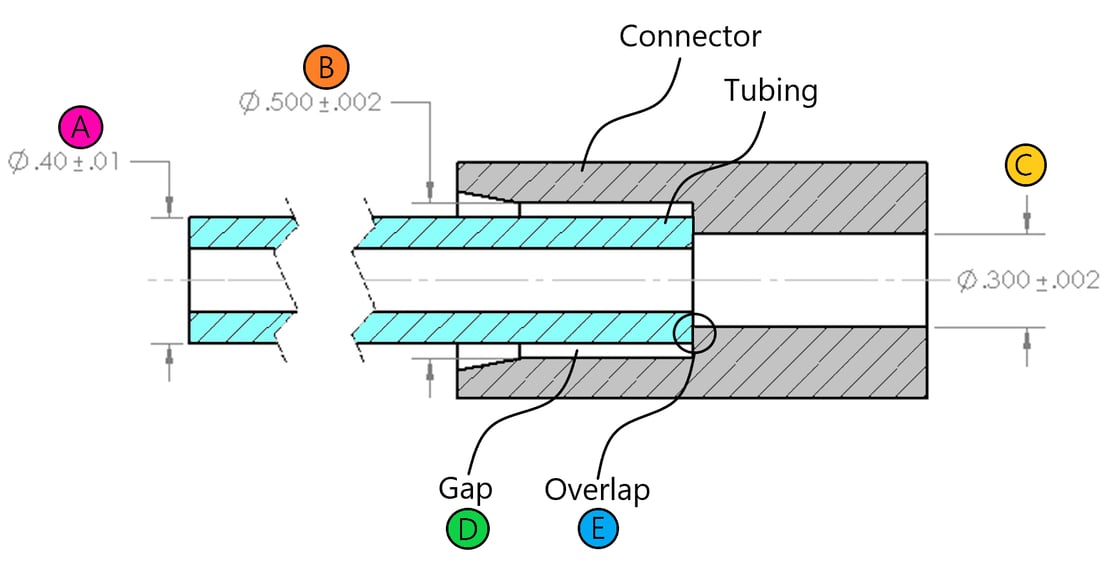
The gap, D, is calculated by subtracting the tubing OD, A, from the connector ID, B, and dividing by 2:
D = (B-A)/2
In order to find the minimum and maximum values for D, you must consider how the minimum and maximum values for A and B will interact:
Dmin = (Bmin-Amax)/2
Dmax = (Bmax-Amin)/2
The overlap, E, is calculated by assuming the tubing can shift completely to one side of the large opening of the connector.
The resulting calculation and equation are as follows:
E+(B-A)-(B-C)/2=0
E=A-B+(B-C)/2
E = A-(B+C)/2
As with finding the range of values for D, you must consider how the minimum and maximum values for A, B, and C will interact:
Emin = Amin-(Bmax+Cmax)/2
Emax = Amax-(Bmin+Cmin)/2
Inserting the initial values for A, B, and C into these equations yields the following results for D and E:
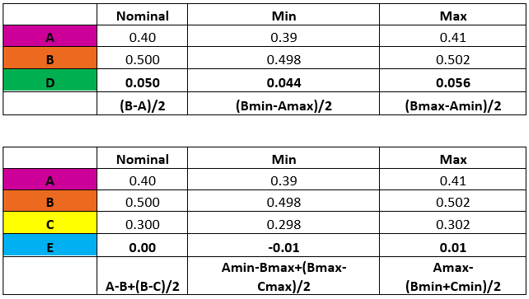
The gap, D, is not close to the required range of .007”-.014”, so the nominal value for A must be increased.
The overlap, E, is nominally zero and in worst case is negative, meaning there is a gap. Tightening the tolerances for A, B and C may help. Tubing tolerances can be held at +/-.005”, and on an injection molded polycarbonate part, +/-.001” is achievable, although there may be an extra charge from each vendor.
Start with looking at increasing nominal value for A:
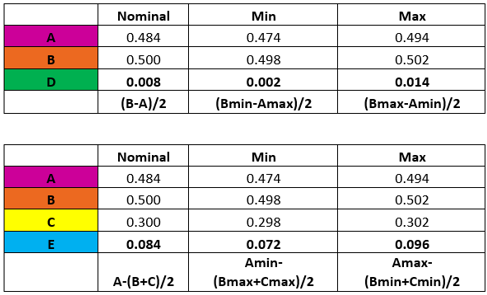The nominal value for D now falls within .007”-.010”, and there is now an overlap, E, in the worst-case scenario, but the range for D is too wide, so examine tightening tolerances for A, B and C:
Now the range of D is close to .007”-.010”, so samples can be assembled and subjected to pull tests to verify that this is an adequate range even though it does not quite reach the requirement. The overlap, E, is positive in all cases meaning no gap is present even in worst case.
There is a possibility that the interaction between the tubing ID and the small ID of the connector is such that the effective, combined ID is small enough to appreciably impact flow. This will not be examined here but is mentioned as an important consideration.
Another important point to mention is that when three or more dimensions interact, such as in the calculation of overlap, E, a statistical case can be made against all dimensions being at the extreme tolerance values at once. In this case you would not use the absolute tolerance values in a stack up calculation, as shown here, but instead an adjusted average value using the RSS or “Root Sum Square” approach. An excellent article on this can be found here:
https://accendoreliability.com/reliability-and-root-sum-squared-tolerances/